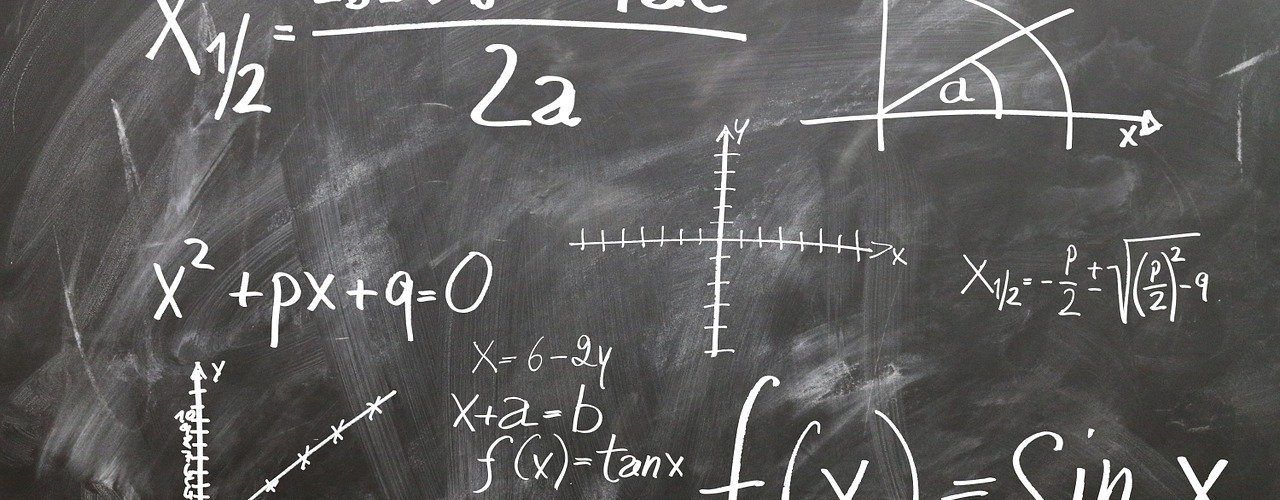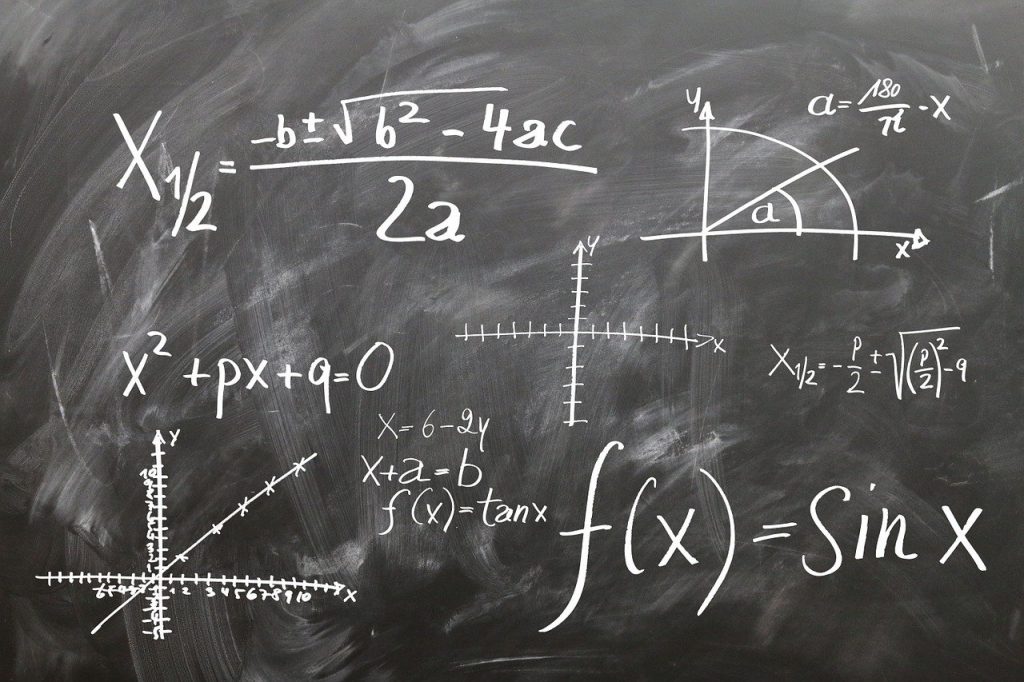
미국 클레이 수학 연구소가 2000년에 발표한 100만 달러 상금이 걸린 문제가 밀레니엄 상금 문제(millennium prize problems)다. 이 중 하나인 리만 가설(Riemann hypothesis)은 소수 분포에 관한 문제로 유명하며 160년 이상 전 세계 수학자를 고민하게 만들고 있다.
소수란 1과 자기 자신으로만 나눠 떨어지는 자연수를 말한다. 기원전 3세기경 고대 그리스 수학자 유클리드는 소수가 무한히 존재한다는 걸 증명했다.
이런 소수의 매력에 빠진 사람이 18~19세기 활약한 독일의 위대한 수학자 카를 프리드리히 가우스였다. 가우스는 10대 시절 300만 개 소수를 써내려가며 표로 정리했다.
가우스는 소수 계량 함수(Prime-counting function)를 연구했다. 소수 계량 함수는 말 그대로 자연수 n에 대해 n 이하 소수 개수를 세는 함수다. 세로축을 소수 계량 함수 π(n), 가로축을 n으로 해 그래프로 나타내면 소수 개수는 1씩 증가하므로 π(n)의 그래프는 마치 계단 모양을 하고 있다. 하지만 n 상한을 아주 크게 잡으면 그래프는 완만한 선 1개처럼 보인다.
가우스는 이 π(n)이 대수적분함수라는 함수와 상당히 가깝다는 걸 발견했다. 다시 말해 자연수 중 소수가 어느 정도 비율로 포함되어 있는지를 대수를 사용해 근사할 수 있다는 것이다. 이게 가우스의 소수 정리(Prime number theorem)다.
그리고 가우스가 활약한 시대보다 조금 거슬러 올라가 18세기 전반에 활약한 수학자 레온하르트 오일러의 업적에 주목한다. 오일러가 남긴 수학적 업적은 위대하고 방대하지만 그 중 하나가 무한급수 탐구다. 무한급수란 무한히 계속되는 수열의 합을 말한다.
예를 들어 1/x의 무한급수는 1/1 + 1/2 + 1/3 + 1/4 +…로 표현된다. 이 1/x의 무한급수는 발산 그러니까 유한한 값에 수렴하지 않는다는 게 증명되어 있다. 하지만 오일러는 1/x²의 무한급수가 π²/6에 수렴한다는 걸 밝혀냈다. 더 나아가 오일러는 1/x⁴의 무한급수가 π⁴/90에 수렴한다는 것도 증명했다.
이런 무한급수를 일반화해 1/x^s의 무한급수=1/1^s + 1/2^s + 1/3^s + 1/4^s +…로 표현되는 함수 ζ(s)가 제타 함수다. 오일러는 이 제타 함수가 소수를 사용한 곱으로 표현될 수 있다는 걸 발견했다. 이를 오일러 곱셈 공식(Euler product)이라고 부른다.
소수와 제타 함수간 연결고리가 보이는 시점에서 등장하는 인물이 가우스의 제자이기도 한 독일 수학자 베른하르트 리만이다. 리만은 이 제타 함수에 복소해석(complex analysis) 개념을 도입했다.
복소해석이란 복소수를 함수에 도입하는 개념. 복소수는 제곱하면 -1이 되는 수 = i를 단위로 하는 허수와 실수로 표현되는 수를 말하며 복소수를 x+yi라는 형태로 나타낼 때 실수 부분(실부)은 x, 허수 부분(허부)은 y가 된다.
ζ(s)는 x > 1일 때 나선을 그리며 유한한 값에 수렴한다. 리만은 해석 접속법(analytic continuation)이라는 방법으로 ζ(s)의 정의역을 확장해 x < 1일 때의 ζ(s)도 고려했다. 이때 s가 -2, -4, -6…과 같은 음의 짝수인 경우, ζ(s) = 0이 된다. 이는 쉽게 증명 가능하므로 음의 짝수가 되는 s는 자명한 영점이라고 불린다. 더 나아가 ζ(s)=0이 되는 s는 0<x<1 범위에도 무한히 많이 존재한다는 것을 알게 됐다. 이 s는 비자명한 영점이라고 불린다. 리만은 비자명한 영점은 x=1/2 선상에만 존재한다고 예상했다. 이게 바로 리만 가설이다.
여기서 가우스가 생각한 소수 정리로 다시 돌아간다. 가우스가 제안한 소수 정리는 소수의 개수를 나타내는 소수 계수 함수와 대수적분함수가 상당히 가깝다는 걸 보여주지만 가깝다는 것은 반드시 오차가 있다는 뜻이다. 리만은 1859년에 발표한 논문 주어진 수보다 작은 소수의 개수에 대하여에서 제타 함수 영점을 사용하면 소수 계수 함수를 더 정밀하게 표현할 수 있다고 생각했다. 다시 말해 리만 가설이 증명되면 소수 분포를 매우 높은 정확도로 구할 수 있게 되는 것이다.
하지만 가설을 제시한 리만 자신은 비자명한 영점이 x=1/2 상에만 존재한다는 가설에 대해 엄밀히 증명되는 게 바람직하지만 스스로 증명을 시도했으나 성과를 얻지 못해 일단은 증명하지 않았다고 논문에 기록했다.
컴퓨터가 발전해 방대한 계산을 고속으로 수행할 수 있게 된 이후 실제로 ζ(s)가 되는 복소수 s가 10조 개나 검증됐다. 그 결과 검증된 모든 비자명한 영점이 x=1/2를 만족한다는 걸 알게 됐다. 컴퓨터의 압도적인 계산력으로 강제로 비자명한 영점을 찾고 있지만 만일 x≠1/2인 비자명한 영점이 발견된다면 그 시점에서 리만 가설이 잘못됐다는 게 된다. 이 방법으로는 리만 가설이 틀렸다는 것을 보일 수는 있어도 리만 가설이 옳다는 것은 증명할 수 없다.
수학자는 160년 이상 리만 가설에 도전하고 있지만 아직 해결에 이르지 못했다. 따라서 1/2<x<1이 되는 s에서 비자명한 영점이 N개 있다고 가정하고 이 N을 0에 가깝게 만들어가는 접근 방식이 취해졌지만 영국의 수학자 알버트 잉엄이 1940년 발표한 논문부터 현대에 이르기까지 거의 진전이 없었다.
2024년 5월 말 MIT 수학자 래리 거스와 옥스퍼드 대학의 제임스 메이나드가 80년 만에 잉엄의 연구 결과에서 한 걸음 더 나아갔다고 주장하는 논문을 미심사 논문 리포지토리인 아카이브(arXiv)에 게재했다. 저명한 수학자인 테렌스 타오는 리만 가설을 향해 놀라운 진전이 있었다면서도 이 가설을 완전히 해결하기에는 아직 멀었다고 언급했다. 관련 내용은 이곳에서 확인할 수 있다.