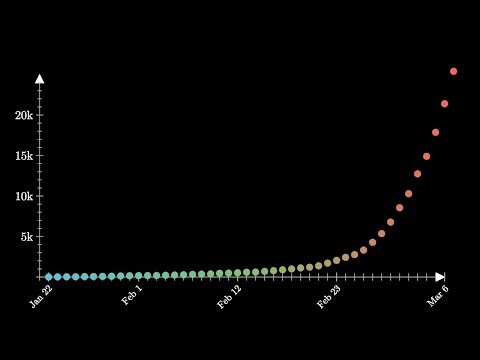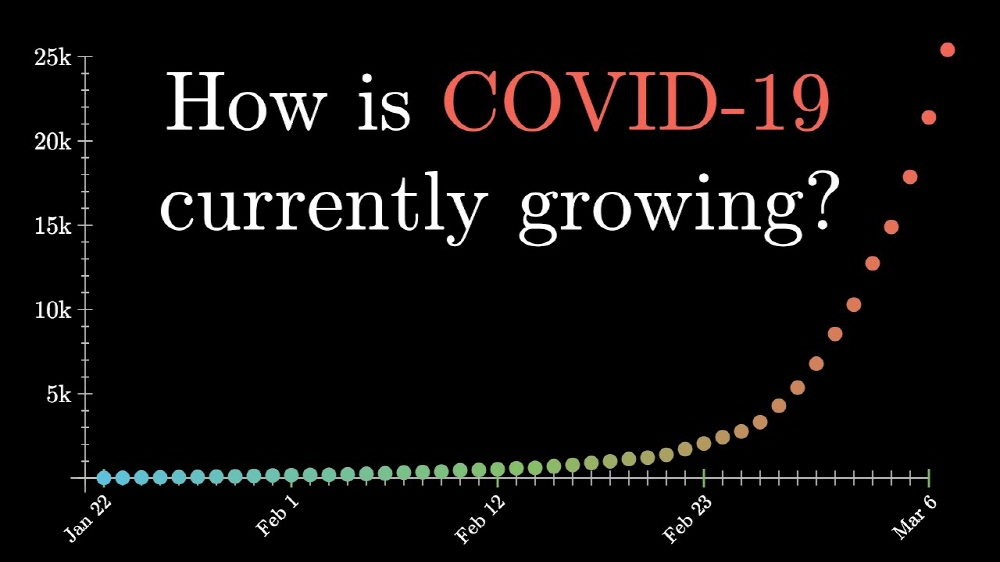
코로나19는 1월 말부터 중국 국외로 유행이 확대되고 있다. 중국을 뺀 지역 내 감염자 수를 정리한 그래프를 유튜브 수학 해설 채널(3Blue1Brown)이 공개하고 1개월 반 만에 기하급수적으로 늘어나고 있다는 걸 설명하고 있다.
영상에서 1월 22일부터 3월 6일까지 중국 본토를 뺀 총 감염자 수 추이를 보면 하루 감염자 수는 전날보다 1.15배에서 1.25배 늘어나 기하급수적으로 증가하고 있다는 지적이다. N은 1일 감염자 수, E는 감염된 사람이 매일 접촉하는 평균 인원수, P는 감염자 접촉에 의해 감염에 이를 확률로 계산하면 1일 새로운 감염자 수는 △Nd=E·p·Nd 식으로 표시할 수 있다. d는 일자를 나타내는 변수다.
이 식을 Nd+1=Nd+E·p·Nd, Nd+1=(1+E·p)Nd로 표현하면 Nd는 어느 날 감염자 수, Nd+1은 1일 이후 감염자 수다. 1+E·p는 감염자 수 증가로 나타낼 수 있다. N은 하루 감염자에서 감염자 수가 많을수록 감염이 빠르게 확대될 수 있다.
얼마나 빠른 속도로 감염자 수가 증가하고 있는지는 20일간 감염자 수가 100명에서 1,000명으로 늘고 다시 13일이면 감염자 수가 1,000명에서 1만명으로 증가한다. 그래프 기울기를 보면 평균적으로 16일마다 감염자 수가 10배가 된다는 예측이 나온다. 만일 앞으로도 16ㅇ일마다 감염자 수가 10배가 된다면 30일 이후에는 그러니까 2020년 4월 5일 경에는 100만명ㅇ, 47일 후인 4월 22일에는 1,000만명, 64일이 지난 5월 9일에는 1억명, 81일 이후인 5월 26일에는 10억명에 도달한다.
물론 이런 증가가 계속된다는 건 아니다. 중증급성호흡기증후군 사스(SARS) 감염자 수는 8,000명에서 수렴하고 스페인 독감은 당시 전 세계 인구 중 27%인 5억명에게 감염되고 수렴됐다. 코로나19로 인한 감염도 어딘가에서 수렴할 가능성이 높으며 문제는 그게 언제가 될지다. 또 감염자 수는 반드시 지구 인구를 초과하지 않는다. 변곡점을 기점으로 증가율은 감소하기 시작한다.
감염자 수가 증가하는 동안 어느 날 감염자 수가 전날 감염자 수로 나눈 성장 인자 1을 초과한 값 그러니까 예를 들어 3월 4일 성장인자는 3월 4일 감염자 2,964명을 3월 3일 감염자 수 2,159명으로 나눈 값 1.37이다. 성장인자가 1을 초과하는 경우에는 로지스틱 곡선은 기하급수적으로 증가하고 1보다 작으면 수렴으로 향한다. 예를 들어 현재 감염자 수가 2만 1,000명으로 성장인자를 1.15로 유지하면 61일 이후 감염자 수는 1억명을 초과할 수 있다. 성장인자가 1.05까지 떨어져도 61일 이후 감염자 수는 40만명이다.
결국 성장인자를 낮추려면 어떻게 하면 좋을지 고민해야 한다. 개인이 여행 등 외출을 피하고 사람이 모이는 곳에 되도록 가지 않고 자주 손을 씻는 등 예방에 힘써야 한다는 것이다.